歷史上有意思的三次數學危機

文史 11-02

原標題：歷史上有意思的三次數學危機

在數學的歷史上，有過三次比較重大的危機，第一次是關於無理數的，這次危機把畢達哥拉斯的數學王朝推翻，第二次數學危機是關於微積分的，是常識跟數學之間的契合的問題；第三次數學危機發生在二十世紀初，這次危機涉及到了數學中最基礎的大廈，差點把整個數學理論推翻重來。下面我來跟大夥聊聊這三次有意思的事件。

畢達哥拉斯

第一次數學危機發生在公元前500年左右，我感覺跟精確度有關，我們平時用到的數學知識，幾乎都只要精確到一定程序就可以了，所以古希臘畢達哥拉斯學派認為，任何一個數都能用a/b的形式來表示，其中a和b都是整數，這些數在數學上有個專有名詞叫有理數。但是有一天，有個叫希帕索斯的學者發現，好像不是這麼回事，他作了一個這樣的假設，就是等腰直角三角形，如果直邊都為1，那麼它的斜邊(√2)就不滿足這個條件。這個證明起來其實很簡單，但是對於當時著了迷的畢達哥拉斯派學者來說，這完全不能接受，就好像發現自己一直深愛的很純潔的美女是綠茶妹一樣，這些氣急敗壞的學者們最後把希帕索斯扔到海裡面去了。這就是典型的學術迫害啊。

紙當然是包不住火的，死了一個希帕索斯，自然會有更多的學者發現√2，√3，√5；第一次數學危機使得純代數的地位下降，幾何學的地位上升，因為幾何量不能完全由有理數來表示，但數卻完全可以用幾何量來表示，從而形成了歐幾里得《原本》的公理體系與亞里士多德的邏輯體系，這兩個體系在經典數學中就有點相牛頓的三大定律。正是因為這次危機，使得東西方數學體系完全走向不同的路，像中國這樣的大國，因為沒有這次數學危機，就沒能完全形成真正的數學體系，儘管很多方面表現得很優秀。

第二次數學危機的發生已經到了十七八世紀，牛頓和萊布尼茲是這次危機的並列第一男主角，第一反派是教會的貝克萊大主教。這次危機的根本問題是微分中關於無窮小的定義，這個無窮小不管是牛大師還是萊大師，對它的定義都很粗糙，甚至於有時候還變來變去，對於一向以嚴謹著稱的數學，顯然是很不合適的。

微積分的創立者牛頓跟萊布尼茲

微積分中的最根本的東西就是這個無窮小，像我們古代祖沖之求∏值，就用到了這個原理，就是把圓的周長解想成包圍他的兩個多邊形周長和的一半，這兩個多邊形的邊數越多（邊長越短，無窮小），計算得越精確；還有卡瓦列里(伽利略的學生)提出了「點動成線，線動成面，面動成體。」的思想。但是這個無窮小到底是個什麼東西，它跟0又是什麼關係，一直都沒有搞清楚，導致產生了一些很有意思的悖論，像典型的龜免賽跑悖論。說的是龜免，如果烏龜先跑100米，烏龜的速度是免子的一半，那麼兔子永遠也追不上烏龜，因為等兔子跑完前面一段a時，烏龜又跑了a/2，邏輯上毫無違和感，但事實上正常人都知道這是不可能的。

附上網上的關於牛頓對於微分的一次證明：

「如果一個物體的運動方程是y=x2（y表示位置，x表示任一時刻），那麼它在任一時刻的速率是怎樣的？」（脫離開「運動」的概念，將y=x2看作函數也可。）

解：第一步：欲求速度v，有一個求平均速率公式：

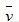
=s/t（速度等於距離除以時間）

第二步：根據運動方程y=x2我們給出一段「微小」運動時間△x=h；那麼這段時間位移量就是

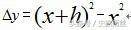
第三步：平均速度

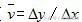
也就是

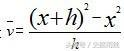
第四步：

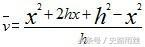
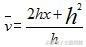
第五步：消去h得

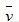
=2x+h

第六步：當這個「微小時間增量h趨近於0時，我們就可以把平均速率看成瞬時速率v」那麼v=2x+0；

得出結論：瞬時速率v=2x

這樣，只要給出任意時刻x，我們就可以很方便的求出任意時刻的瞬時速率v了！

但是，以上計算出現了一個明顯的邏輯悖論——「微小量h」是什麼？

「如果h是0，那麼第三步中不能做分母；如果h不是0，第六步怎麼又等於0了？」

對於微積分，我前段時間有個想法，就是把它跟物理學的量子力學聯繫起來，用來解釋量子力學中某些經典力學不能解釋的現象，像測不準原理。點動為線，線動為面，那麼量子力學中微小粒子測不準是不是也是因為跟我們不在一個維度上面，所以它的數據我們測量得不精確，而並不是真正意義上的測不準。像f(x)=2x,那麼它的積分公式將是f(x)=x的平方+h，其中h為一個常量，但這個常量是多少，需要具體問題具體分析。不過因為我水平有限，一直沒能理明白，到底是否真實存在聯繫。

第三次數學危機發生在十九世紀下半部分，第一男主角是群論（集合論）的創立者康托爾，第一反派是大數學家羅素。

康托爾

集合論真的很牛，但也很簡單，記得我第一次看集合論的時候，被它的簡單，但功能強大完全驚呆了。像證明自然數和奇數一樣多，就是構建兩個無窮集合A（自然數），B（奇數）（自然數跟奇數都是無窮集合的），A中任何一個數n都能在B中找到對應的2n+1,反之亦成立，所以A=B。要是用其它數學理論去證明，這得多複雜，但集合論，就這麼簡單完美地解決了。